浅谈跳表 | 青空之蓝

为什么使用跳表

**跳表是（skip list）**Redis 实现 sorted set 使用的数据结构，是一种平衡数据结构，其中常用的数据结构有：B 树，AVL 树，红黑树等，如果你了解过这些平衡结构，你或许会有个疑问，为什么要使用跳表？想象一下，给你一支笔，一张纸，一个编辑器或者 IDE，你能在短时间内写出一个红黑树或者 AVL 树？这很难吧。而跳表，我们只需要对链表稍加改造就可以支持快速增删改查，使用类似于二分搜索的查找算法，而这种数据结构就是跳表。它的效率和红黑树以及 AVL 树不相上下。

什么是跳表

首先我们先来看一个链表：

对于这种链表来说，即使链表之中是有序的，如果我们要从中查找某个值，也只能从头逐个查找，运气好的话查找一次就能找到，运气差的话或许要查找 n 次。在使用数组存储的方式中我们可以通过二分搜索来快速的查找某个值，而链表由于不支持随机查询，所以就不能使用二分搜索的方式来查找。

那么如何能提高查找效率呢？在 O(n)的时间复杂度下如果要提高运行效率，二分是必不可少的，树结构可以通过左右子树来分区，那链表又如何分区呢？建立索引，我们对这个链表加上一层索引。

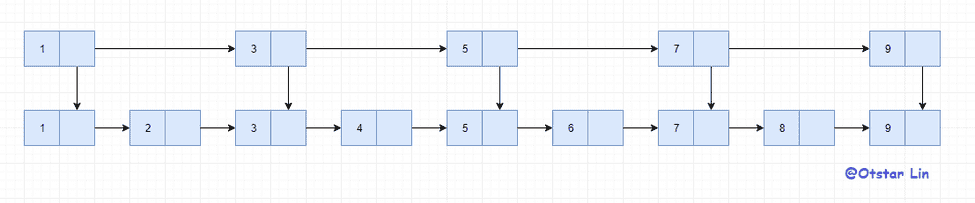
假如我们要查找 6，只需要走 1->3->5->6，减少了 2 步，那如果我们再加几层索引呢？

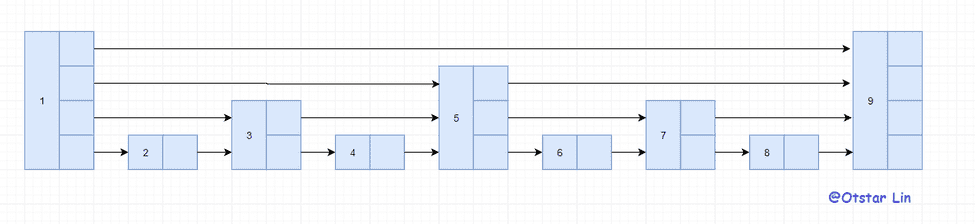
这时的查找其实就是二分查找了，查找效率已经有质的提升。而这种的原理其实很简单就是通过分区来跳过大量的节点。

上面所说的结构是静态的，当我们向上方的跳表中不断加入数据，如果不更新索引就有可能出现某节点之间出现大量节点的情况，在极端的情况下还会退化成链表。而如果在插入的时候重建索引那势必会导致跳表的插入效率大幅下降。那要如何解决动态插入的问题呢？在红黑树和 AVL 树中是使用左右旋来平衡二叉树，而跳表同样也有一种机制来平衡：通过随机函数来是插入的节点的层高是随机的，不强制要求 1：2 的分区。如，我们要在以下的跳表中添加一个值为 18 的节点：

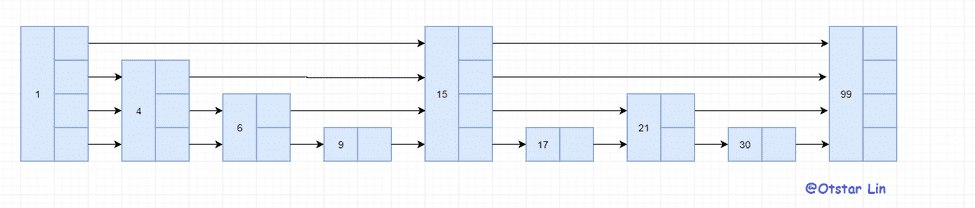
首先我们需要通过一个随机函数来得出新节点的层高。假设在这次插入中得到的层高是 3

public int randomLevel() {
    int level = 1;
    for (int i = 1; i < this.maxLevel; ++i) {
        if (this.r.nextInt() % 2 == 1) {
            level++;
        }
    }
    return level;
}

public int randomLevel() {
    int level = 1;
    for (int i = 1; i < this.maxLevel; ++i) {
        if (this.r.nextInt() % 2 == 1) {
            level++;
        }
    }
    return level;
}

然后搜索到插入的位置。

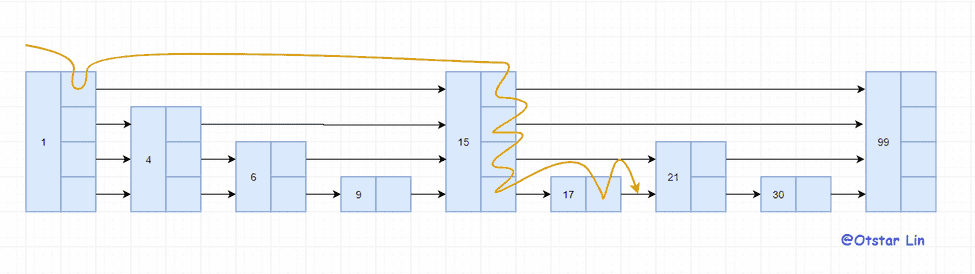
最后将节点插入并重新设置指针，从上一张图中我们可以看到游标走了所有的层，而游标在游走的时候就可以记录层信息，就可以重设指针了。

简单分析跳表效率

从上面图中我们可以知道，大致每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，也就是说，第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2，那第 k级索引结点的个数就是 n/(2k)。那么假设层数足够高，即最高层只有两个节点，那么可知 n/(2k)=2，即 k=log2n-1，若把原始链表计算在内那 k=logn，若每次查找都要下降 m 层的时候，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。而 m 可以认为是参数，所以跳表查询一个数据的时间复杂度就为 O(logn)。

说完时间，那么我们来说说空间，比起链表和二叉树，跳表需要多个指针域，肯定需要比链表和二叉树多许多空间。若我们两个节点就提升一层，那需要的索引数量就为 n/2+n/4+n/8+...+2，即 n-2，所以可以知道跳表所用的空间复杂度为 O(n)，看起来似乎很大？但是我们需要考虑原始链表中数据存储的大小，若数据的大小很大，那么索引使用的空间就微不足道了。

实现代码

忘记附上代码了，逃

package MySkipListDemo;

import java.lang.reflect.Array;
import java.util.Random;
import java.util.Scanner;

/**
 * MySkipListDemo
 */
public class MySkipListDemo {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // SkipList list = new SkipList();
        MySkipList<Integer, Integer> list = new MySkipList<Integer, Integer>();
        list.insert(3, 3);
        list.insert(1, 1);
        list.insert(2, 2);
        list.insert(4, 4);
        list.insert(15, 15);
        list.insert(5, 5);
        list.insert(6, 6);
        list.insert(16, 16);
        list.insert(17, 17);
        list.insert(7, 7);
        list.insert(8, 8);
        list.insert(9, 9);
        list.insert(13, 13);
        list.insert(10, 10);
        list.insert(11, 11);
        list.insert(20, 20);
        list.insert(12, 12);
        list.insert(15, 15);
        list.insert(18, 18);
        list.insert(19, 19);
        list.remove(1, 1);
        list.remove(10, 10);
        list.remove(20, 20);
        list.printAll();
        in.close();
    }
}

/**
 * MySkipList
 */
class MySkipList<K extends Comparable<K>, V extends Comparable<V>> {
    int maxLevel = 16;
    int currLevel = 0;
    boolean keySort = true;
    boolean isMax = false;

    Node head = null;

    private Random r = new Random();

    class Node {
        Node[] next;
        K key;
        V value;
        int level;

        Node() {
        }

        @SuppressWarnings("unchecked")
        Node(K key, V value, int level) {
            this.next = (Node[]) Array.newInstance(Node.class, level);
            this.key = key;
            this.value = value;
            this.level = level;
        }

        public String toString() {
            return "[" + key + "," + value + "](" + level + ")";
        }
    }

    MySkipList() {
    }

    MySkipList(int maxLevel, boolean keySort, boolean isMax) {
        this.maxLevel = maxLevel;
        this.isMax = isMax;
        this.keySort = keySort;
    }

    public int randomLevel() {
        int level = 1;
        for (int i = 1; i < this.maxLevel; ++i) {
            if (this.r.nextInt() % 2 == 1) {
                level++;
            }
        }
        return level;
    }

    public void insert(K key, V value) {
        this.add(key, value);
    }

    @SuppressWarnings("unchecked")
    public void add(K key, V value) {
        if (this.head == null) {
            head = new Node(key, value, maxLevel);
            return;
        }
        if (this.head.key.compareTo(key) == (this.isMax ? -1 : 1)) {
            K tempKey = head.key;
            V tempValue = head.value;
            head.value = value;
            head.key = key;
            value = tempValue;
            key = tempKey;
        }
        int level = this.randomLevel();
        Node p = head;
        Node update[] = (Node[]) Array.newInstance(Node.class, level);
        Node newNode = new Node(key, value, level);
        for (int i = level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
            update[i] = p;
        }
        for (int i = 0; i < level; ++i) {
            newNode.next[i] = update[i].next[i];
            update[i].next[i] = newNode;
        }

        if (currLevel < level)
            currLevel = level;
    }

    @SuppressWarnings("unchecked")
    public void remove(K key, V value) {
        Node p = head;
        if (p.key.compareTo(key) == 0) {
            head.key = head.next[0].key;
            head.value = head.next[0].value;
            Node rNode = head.next[0];
            for (int i = 0; i < rNode.level; i++) {
                head.next[i] = rNode.next[i];
            }
            return;
        }
        Node update[] = (Node[]) Array.newInstance(Node.class, p.level);
        for (int i = p.level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
            update[i] = p;
        }
        if (p.next[0] != null && p.next[0].value.compareTo(value) == 0) {
            Node rNode = p.next[0];
            for (int i = 0; i < rNode.level; i++) {
                update[i].next[i] = rNode.next[i];
            }
        }
    }

    public Node search(K key, V value) {
        Node p = head;
        if (p.key.compareTo(key) == (this.isMax ? -1 : 1)) {
            return null;
        } else if (p.key.compareTo(key) == 0) {
            return p;
        }
        for (int i = p.level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
        }
        if (p.next[0] != null && p.next[0].value.compareTo(value) == 0) {
            return p.next[0];
        } else {
            return null;
        }
    }

    public void printAll() {
        Node p = head;
        while (p != null) {
            System.out.println(p);
            p = p.next[0];
        }
    }
}

package MySkipListDemo;

import java.lang.reflect.Array;
import java.util.Random;
import java.util.Scanner;

/**
 * MySkipListDemo
 */
public class MySkipListDemo {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // SkipList list = new SkipList();
        MySkipList<Integer, Integer> list = new MySkipList<Integer, Integer>();
        list.insert(3, 3);
        list.insert(1, 1);
        list.insert(2, 2);
        list.insert(4, 4);
        list.insert(15, 15);
        list.insert(5, 5);
        list.insert(6, 6);
        list.insert(16, 16);
        list.insert(17, 17);
        list.insert(7, 7);
        list.insert(8, 8);
        list.insert(9, 9);
        list.insert(13, 13);
        list.insert(10, 10);
        list.insert(11, 11);
        list.insert(20, 20);
        list.insert(12, 12);
        list.insert(15, 15);
        list.insert(18, 18);
        list.insert(19, 19);
        list.remove(1, 1);
        list.remove(10, 10);
        list.remove(20, 20);
        list.printAll();
        in.close();
    }
}

/**
 * MySkipList
 */
class MySkipList<K extends Comparable<K>, V extends Comparable<V>> {
    int maxLevel = 16;
    int currLevel = 0;
    boolean keySort = true;
    boolean isMax = false;

    Node head = null;

    private Random r = new Random();

    class Node {
        Node[] next;
        K key;
        V value;
        int level;

        Node() {
        }

        @SuppressWarnings("unchecked")
        Node(K key, V value, int level) {
            this.next = (Node[]) Array.newInstance(Node.class, level);
            this.key = key;
            this.value = value;
            this.level = level;
        }

        public String toString() {
            return "[" + key + "," + value + "](" + level + ")";
        }
    }

    MySkipList() {
    }

    MySkipList(int maxLevel, boolean keySort, boolean isMax) {
        this.maxLevel = maxLevel;
        this.isMax = isMax;
        this.keySort = keySort;
    }

    public int randomLevel() {
        int level = 1;
        for (int i = 1; i < this.maxLevel; ++i) {
            if (this.r.nextInt() % 2 == 1) {
                level++;
            }
        }
        return level;
    }

    public void insert(K key, V value) {
        this.add(key, value);
    }

    @SuppressWarnings("unchecked")
    public void add(K key, V value) {
        if (this.head == null) {
            head = new Node(key, value, maxLevel);
            return;
        }
        if (this.head.key.compareTo(key) == (this.isMax ? -1 : 1)) {
            K tempKey = head.key;
            V tempValue = head.value;
            head.value = value;
            head.key = key;
            value = tempValue;
            key = tempKey;
        }
        int level = this.randomLevel();
        Node p = head;
        Node update[] = (Node[]) Array.newInstance(Node.class, level);
        Node newNode = new Node(key, value, level);
        for (int i = level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
            update[i] = p;
        }
        for (int i = 0; i < level; ++i) {
            newNode.next[i] = update[i].next[i];
            update[i].next[i] = newNode;
        }

        if (currLevel < level)
            currLevel = level;
    }

    @SuppressWarnings("unchecked")
    public void remove(K key, V value) {
        Node p = head;
        if (p.key.compareTo(key) == 0) {
            head.key = head.next[0].key;
            head.value = head.next[0].value;
            Node rNode = head.next[0];
            for (int i = 0; i < rNode.level; i++) {
                head.next[i] = rNode.next[i];
            }
            return;
        }
        Node update[] = (Node[]) Array.newInstance(Node.class, p.level);
        for (int i = p.level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
            update[i] = p;
        }
        if (p.next[0] != null && p.next[0].value.compareTo(value) == 0) {
            Node rNode = p.next[0];
            for (int i = 0; i < rNode.level; i++) {
                update[i].next[i] = rNode.next[i];
            }
        }
    }

    public Node search(K key, V value) {
        Node p = head;
        if (p.key.compareTo(key) == (this.isMax ? -1 : 1)) {
            return null;
        } else if (p.key.compareTo(key) == 0) {
            return p;
        }
        for (int i = p.level - 1; i >= 0; i--) {
            while (p.next[i] != null && p.next[i].key.compareTo(key) == (this.isMax ? 1 : -1)) {
                p = p.next[i];
            }
        }
        if (p.next[0] != null && p.next[0].value.compareTo(value) == 0) {
            return p.next[0];
        } else {
            return null;
        }
    }

    public void printAll() {
        Node p = head;
        while (p != null) {
            System.out.println(p);
            p = p.next[0];
        }
    }
}

结语

跳表的时间复杂度是 O(logn)，空间复杂度是 O(n)，虽然不如平衡树来的“高效”，但是跳表的实现非常灵活，可以有效的平衡执行效率和内存消耗，并且实现起来也比平衡树容易，所以多数情况下跳表会是比平衡树更好的选择。

浅谈跳表

https://blog.ixk.me/post/talking-about-skip-list

许可协议
BY-NC-SA
本文作者
Otstar Lin
发布于
2019/09/14

转载或引用本文时请遵守许可协议，注明出处、不得用于商业用途！