算法复杂度分析(1)

为什么需要算法复杂度分析，实际运行一遍然后收集运行的信息和统计不就可以了？这总事后分析的方法确实没有错，但是当环境发生变化，数据量发生变化，或者数据模型改变了，程序的执行效率就有可能发生巨大的改变，所以我们需要一种粗略的，不需要具体测试数据的估算程序执行效率的方法，而这种方法就是复杂度分析。

大 O 复杂度表示法

大 O 表示法是一种特殊的表示法，指出了算法的速度有多快或者多慢。谁在乎呢？实际上，你经常要使用别人编写的算法，在这种情况下，知道这些算法的速度大有裨益。

这里我们拿一段代码来进行解释：

int fun(int n) {
    int num = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

int fun(int n) {
    int num = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

这段代码是用来求数列和的，我们把每一句代码执行的时间记为 1u，然后默认每句基础代码执行的时间都是一样的，从上面的代码我们可以看出，int num = 0;和int i = 1;各执行了 1 次，sum = sum + i;和i++各执行了 n 次，return部分我们不看，那么这个函数所执行的总时间就应该是(2n+2)*1u，我们把总时间记为 T(n)那么，可以看出执行的总时间和 n 成正比关系，即和执行次数成正比关系，而这种规律我们可以总结成一个公式即:

T(n) = O[f(n)]

而上一个公式就可以表示成T(n) = O(2n+2)，当 n 到大一定程度的时候我们就可以把+2 和 n 的系数 2 给忽略掉，这时候的T(n) = O(n)，这就是我们常说的 O(n)时间复杂度或 O(n)空间复杂度的由来。

时间复杂度分析

那么当代码越来越长，越来越庞大是时候难道还这样一步步分析吗？当然不是，当我们对算法或者程序进行分析的时候我们只需要关注以下几点即可：

1. 只关注循环次数最多的代码

还是拿上面一段代码来分析。

int fun(int n) {
    int num = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

int fun(int n) {
    int num = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

从代码中我们可以看出，只有一个循环 n 次的 for 循环，而其他部分的代码只执行了一次，这时我们就可以直接忽略掉那些只执行一次的代码，只关注执行最多的代码，即 for 循环中的代码，所以这个函数的时间复杂度就是 O(n)。

2. 加法法则：只关注执行次数最多的代码的时间复杂度

int fun(int n) {
    for (int i = 0; i < 10; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n*10; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n*n; i++) {
        System.out.println("a");
    }
}

int fun(int n) {
    for (int i = 0; i < 10; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n*10; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n*n; i++) {
        System.out.println("a");
    }
}

从上面的代码我们可以看到 4 个 for 循环这时候应该如何判断呢？首先我们先找出它们各自循环了几次，第一个执行了 10 次，第二个执行了 n 次，第三个执行了 10n 次，第四个执行了 n2 次，这时候我们只需要关注执行最多的那个循环的复杂度即可，即第四次（我们均默认 n 很大），所以这段函数的时间复杂度为 O(n2)。

3. 乘法法则：嵌套代码的时间复杂度等于嵌套内外的时间复杂度的乘积

int fun(int n) {
    for (int i = 0; i < n; i++) {
        cal(n);
    }
}

int cal(int n) {
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
}

int fun(int n) {
    for (int i = 0; i < n; i++) {
        cal(n);
    }
}

int cal(int n) {
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
}

从上方代码看出，fun 函数中的 for 循环每次循环都需要调用一次 cal 函数，而我们可以很轻松的判断出 cal 函数的时间复杂度是 O(n)，而 fun 一共需要调用 n 次 cal 函数，即 O(n) * O(n)，即 O(n*n)，简化下就是 O(n2)。

到这里我们就基本讲完了时间复杂度的分析方法了，下面我们就来看以下几种常见 的算法时间复杂度。

番外：常见的时间复杂度

1. O(1)

这个时间复杂度并不是表示只有一句基础代码，而是代表常数的时间复杂度，即使你有 100 句基础代码也不能表示为 O(100)，而应该表示为 O(1)。

2. O(logn), O(nlogn)

对数阶时间复杂度非常常见，同时也是最难分析的一种时间复杂度。 我这里就拿算法图解这本书中的一张图来说明：

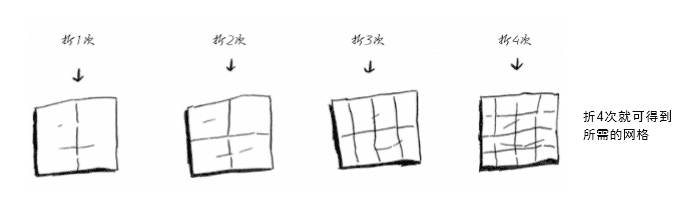
来自《算法图解》

我们要得到一张 16 格的纸，如果采用对半折的方式就只需要 4 次就能完成，即 4 = log216 若把 4 换成 T(n)，16 换成 n，我们就可以得到 T(n) = O(log2n)，然后我们忽略掉常数的底数，就变成了 O(logn)，并不是只有 2 才能忽略掉底数，所有的常数底数都可以被忽略。

3. O(m+n)、O(m*n)

或许你有看过这种复杂度，或许没有看过，这种其实非常简单，我们通过下面的例子来进行分析：

int fun(int m, int n) {
    for (int i = 0; i < m; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
}

int fun(int m, int n) {
    for (int i = 0; i < m; i++) {
        System.out.println("a");
    }
    for (int i = 0; i < n; i++) {
        System.out.println("a");
    }
}

当我们看到这个函数的时候是不是就应该通过加法法则排除掉一个呢？然后你会发现若不知道 m 和 n 的大小关系根本无法对其进行判断，也就无法排除掉其中的一项，这时候就应该保留两个未知数，即 O(m + n)，另外的 O(m * n)同理。

空间复杂度分析

空间复杂度的分析十分的简单，我们直接通过一个例子来进行分析吧：

int fun(int n) {
    int[] arr = new int[n];
    return arr;
}

int fun(int n) {
    int[] arr = new int[n];
    return arr;
}

这段例子非常简单，就是创建了一个大小为 n 的数组，所以这段代码的时间复杂度就是 O(n)。

结语

复杂度的分析其实不难，只要多练习，多分析就能熟练的掌握它，还有最好时间复杂度，最坏时间复杂度，以及平均时间复杂度等一些分析我留着下一篇在说吧，零零散散的写了一篇文章，还是挺累的，完全手打了 2300+个字，其实是懒 （逃，(￣ y▽,￣)╭ 。